
|
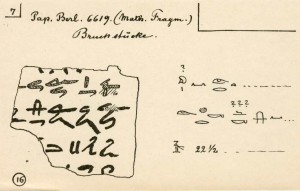
El papiro matemático de Berlin ( 6619) fue comprado en 1850, en Luxor, por A. H. Rhind - a la vez que el papiro de Rhind. Este papiro se encontraba en peor estado siendo analizado y restaurado 50 años mas tarde por Schack-Schackenburg. Se encuentra actualmente, en el Staatliche Museum de Berlin.
En este papiro aparece por primera vez la solución de una ecuación de 2º grado.
|
|
Problema: Se dice que el área de un cuadrado de 100 m. cuadrados es igual a la suma de las áreas de otros dos cuadrados mas pequeños. El lado de uno de ellos es 1/2+1/4 del otro otro. Cual es la medida de los lados de los dos cuadrados?
Solución:
Actualmente, sabemos que este problema se resuelve a través do sistema de equaciones:
x²+y² = 100,
y = (1/2+1/4)x
en que x e y son los lados de los cuadrados que pretendemos conocer.
x²+y² = 100,
y = (1/2+1/4)x
en que x e y son los lados de los cuadrados que pretendemos conocer.
Solución:
Actualmente, sabemos que este problema se resuelve a través do sistema de equaciones:
x²+y² = 100,
y = (1/2+1/4)x
en que x e y son los lados de los cuadrados que pretendemos conocer.
x²+y² = 100,
y = (1/2+1/4)x
en que x e y son los lados de los cuadrados que pretendemos conocer.
Veamos la resolución presentada en el papiro.
Supongamos que uno de los dos cuadrados tiene un lado de 1 meh. El lado del otro cuadrado será, entonces, de 1/2+1/4 de meh. Las áreas serán: para el primero 1 meh cuadrado y para el segundo1/2+1/16 de meh cuadrado. Entonces la suma de las áreas de los dos cuadrados es 1+1/2+1/16 de meh quadrado. La raiz cuadrada de esta suma es 1+1/4.
Como la raíz cuadrada de 100 es 10 debemos encontrar un número N tal que multiplicado por 1+1/4 nos de 10, o sea, tenemos que dividir 10 por 1+1/4. Así, N = 8. Por tanto, x = 8 e y = (1/2+1/4).8 = 6, o sea, un cuadrado tendrá de lado 8 meh y otro 6 meh.
Data aproximadamente de 1800 a.C. y se conserva en el Museu Staatliche em Berlim.
Neste papiro aparece pela primeira a solução de uma equação do 2º grau. Dois dos seus problemas, apresentados a seguir, dão origem a um sistema de duas equações, sendo uma delas uma equação do 2º grau. Na notação actual os sistemas de equações envolvidos nos problemas são:
x2 + y2 = 100 e 4x - 3 y = 0 (1)
x2 + y2 = 400 e 4x - 3 y = 0 (2)
Problema (1)
É te dito … a área de um quadrado de 100 [cúbitos quadrados] é igual à de dois quadrados mais pequenos. O lado de um dos quadrados é ½ + ¼ o lado o outro. Diz-me quais são os lados dos dois quadrados desconhecidos.
Resolução:
Toma sempre o quadrado de lado 1. Então o lado do outro é ½ + 2/4.
Multiplica-os por ½ + 2/4. Dá ½ + 1/16, área do quadrado pequeno. Depois juntos estes quadrados têm uma área de 1 + ½ + 1/16.
Tira a raiz quadrada de 1 + ½ + 1/16. Que é 1 + ¼.
Tira a raiz quadrada de 100 cúbitos. Que é 10.
Divide estes 10 por 1 + ¼. Dá 8, o lado de um quadrado.
Calcula ½ + ¼ de 8. Dá 6, o lado do outro quadrado. (citado por Gillings)
Problema (2)
É te dito … a área de um quadrado de 400 [cúbitos quadrados] é igual à de dois quadrados mais pequenos. 1 + ½ do lado de um dos quadrados é o dobro do lado do outro. Diz-me quais são os lados dos dois quadrados desconhecidos.(adaptado de Gillings)
Este y otros papiros Prisse, Westcar etc…en mi página web: www.uned.es/…/papiro%20de%20ani.htm. Aviso:Aquí en el blog no funcionan los links, allí sí.
Filed under: ACTUALIDAD,Arqueologia,Exposiciones,H. Egipto,HISTORIA ANTIGUA
Trackback Uri